[Java]최장 증가 부분 수열(LIS, Longest Increasing Subsequence)

*최장 증가 부분 수열(LIS, Longest Increasing Subsequence)

->최장 증가 부분 수열이란, 주어진 수열에서 오름차순으로 정렬된 가장 긴 부분 수열을 찾는 문제이다. 여기서 부분 수열은 연속적이거나, 유일할 필요는 없다.

->아래 그림을 참고하여 이해하도록 하자.

증가하는 부분 수열. 수열이 연속적일 필요는 없다.

최장 증가 부분 수열. 해당 수열에서 찾을 수 있는 가장 긴 부분 수열이다.

 해당 예시로 주어진 배열에서는 가장 긴 증가하는 부분 수열(이하 LIS)은 1, 2, 3, 7임을 직관적으로 알 수 있다.

->LIS를 구하는 문제는 Knapsack, LCS와 더불어 다이나믹 프로그래밍의 기초를 다지는데 자주 사용되는 예제 중 하나이다. 이 문제 역시 백준 Silver2 11053 가장 긴 증가하는 부분 수열 문제를 기반으로 알고리즘을 설명하도록 하겠다.

※ 문제 주소 : https://www.acmicpc.net/problem/11053

11053번: 가장 긴 증가하는 부분 수열

※ 이 문제 역시 백 트래킹을 활용하여 문제를 해결할 수 있지만, 해당 풀이는 O(2^N)의 시간 복잡도를 갖기도 하고 Knapsack Problem과 유사한 논리를 바탕으로 풀이할 수 있기 때문에 생략하도록 하겠다.

 

*동적 계획법을 활용한 풀이 : O(N^2)

->먼저, 비교적 이해하기 쉬운 동적 계획법을 활용한 풀이를 바탕으로 문제를 해결해보자. 해당 풀이는 O(N^2)의 시간 복잡도를 가지고 있다.

->Knapsack Problem과 마찬가지로 해당 블로그에 포스팅한 '동적 계획법 접근 방식'을 바탕으로 문제에 접근해보겠다.

※ 참고 : https://sskl660.tistory.com/87

[Java]동적 계획법(Dynamic Programming)

 

1. 문제를 특정한 부분 문제로 생각해보고, 해당 문제를 저장할 dp 테이블을 정의해본다.

(1) 해당 수열의 i번째 원소의 위치에서 가질 수 있는 LIS의 값은 무엇일까?

->문제에 따르면 수열의 크기가 N인 배열이 입력으로 주어질 것이고, 우리는 우선 간단하게 N개의 원소 중 1번째, 2번째, 3번째... N번째 위치 해당 원소가 가질 수 있는 LIS의 값을 부분 문제로 생각해볼 수 있다.

->따라서, 해당 위치에서 해당 원소가 가질 수 있는 LIS의 값을 저장할 1차원 dp 테이블을 만들고 문제에 접근해보자. 아래 그림을 참고하도록 하자.

dp 테이블의 원소의 값은 배열의 해당 위치의 원소에서 가질 수 있는 LIS의 값을 의미한다.

->우선, 첫 번째 원소부터 생각해보자. 10이라는 원소가 가질 수 있는 LIS의 값은 우선 본인 그 자체의 길이를 생각할 수 있다. 따라서 dp[1]의 값은 1로 채울 수 있음을 알 수 있다.

->다음으로 두 번째 원소 20을 살펴보자. 우선, 첫 번째 원소와 마찬가지로, 20은 본인 그 자체의 길이를 바탕으로 초기화가 가능하기 때문에 1이라는 값으로 초기화할 수 있음을 알 수 있다. 이로부터 우선 해당 테이블의 원소에 dp 값을 채울 때 원소의 값을 1로 초기화할 수 있음을 유추해볼 수 있다.

  하지만 우리는 우선 직관적으로 해당 위치에서 LIS의 값이 1로 설정되면 안된다는 것을 알고있다. 이전 원소(10)에 비하여 증가하는 상태이므로 해당 위치의 값은 2로 설정되어야 한다는 것을 알 수 있다. 

 우선 이 단계에서 부터 지금까지 기억해둔 dp 테이블에 저장된 값과 비교하여 규칙성을 찾을 수 있다면 좋겠지만 그 관계를 유추하기 쉽지 않을 것이다. 우선 다른 원소들도 차근차근 채워보자.

->다음으로 세 번째 원소인 10을 살펴보자. 마찬가지로 본인의 길이를 바탕으로 해당 위치를 1로 설정한다.

 

 두 번째 원소를 채울 때와는 다르게, 해당 위치에서는 직관적으로 보아도 그 값이 갱신될 가능성이 없어보인다. 따라서, 해당 테이블은 1로 채우고 넘어갈 수 있음을 알 수 있다.

->다음으로 네 번째 원소인 30을 살펴보자. 마찬가지로 해당 위치는 1로 초기화가 가능할 것이다.

 하지만 직관적으로 보았을 때, 해당 위치는 10, 20이후 30이라는 증가된 부분 수열을 이룰 수 있는 위치이기 때문에 해당 위치의 값이 3이 되어야 한다는 것을 알 수 있다.

  자, 이제 규칙성을 파악해보자. 우선 dp 테이블에 저장되는 값은 해당 원소의 위치에서 가질 수 있는 LIS의 값이었다는 것을 잊어서는 안된다. 그렇다면 그 값 들을 어떻게 활용할 수 있을까?

 우선 30이라는 값은 앞선 원소들(10, 20, 10)에 비하여 큰 값을 가지고 있음을 알 수 있다. 즉, 어떤 원소가 오더라도 해당 원소 뒤에 추가 되면서 최장 증가 부분 수열이 될 수 있음을 나타낸다고 이해할 수 있다. 근데 우리가 dp 테이블에 저장한 값은 해당 원소의 위치에서 가질 수 있는 LIS의 길이였다. 즉, 해당 위치에서 앞 원소들에 비하여 증가할 가능성이 존재한다면, 해당 위치의 LIS의 값에 자신의 길이를 +1 해주면 된다는 것을 파악할 수 있다.

 즉, 다시 처음부터 자신의 길이인 1로 채우는 경우(초기화)부터 생각해보자.

 우선 1번째 원소(10)에 대하여 30이라는 수는 부분 수열의 길이를 증가시킬 수 있으므로 dp[1] + 1의 값을 dp[4]의 값 후보에 올릴 수 있다.

 마찬가지로 2, 3번째 원소(20, 10)에 대하여 30이라는 수는 부분 수열의 길이를 증가시킬 수 있으므로 dp[2] + 1, dp[3] + 1의 값을 dp[4]의 값 후보에 올릴 수 있다.

 자, 그렇다면 이제 본인의 길이 1과 1, 2, 3번째 원소에 대하여 본인을 추가시킨 LIS의 길이 중 가장 큰 값은 무엇인가? 이는 2번째 원소로부터 본인의 길이를 추가시킨 3이 될 것임을 알 수 있다. 따라서 해당 위치의 값은 3이 되는 것이다.

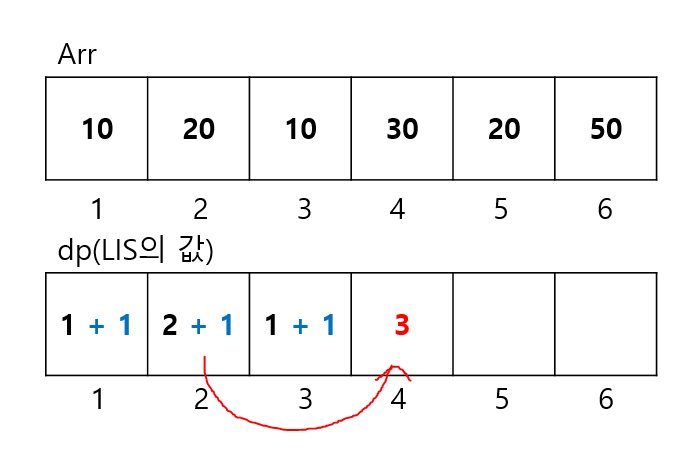
->다음으로 5번째 원소인 20에 대하여 생각해보자. 앞선 논리를 이해했다면 해당 규칙을 그대로 적용시키기만 하면 5번째 원소의 위치에서의 LIS의 값은 쉽게 구할 수 있다. 우선, 본인의 길이인 1로 해당 원소의 값을 채운다.

 이때, 20이라는 값은 앞선 원소(10, 20, 10, 30)에 대하여 그 값이 10인 경우(1번째, 3번째 원소)에 대해서만 부분 수열의 길이가 증가할 가능성이 있다. 따라서, 해당 위치의 LIS의 값에 본인의 길이를 + 1한 경우만 후보에 올라갈 수 있다.

 당연히 이 값 중 가장 큰 값은 2가 될 것이고, 해당 위치에는 2라는 값으로 채워질 것임을 알 수 있다. 직관적으로 보아도 해당 위치에서 가질 수 있는 LIS의 값은 2가 되는 것을 알 수 있다.

->마지막 원소인 50역시 마찬가지 논리로 생각하면 dp[4]의 값을 활용하여 최종적으로 dp[6] = 4가 됨을 알 수 있다.

 

2. 부분 문제의 관계를 생각하며 점화식을 도출한다.

->위의 규칙성을 점화식으로 세워보자. 우선, 해당 원소의 위치에 방문할 때 마다 해당 위치의 길이는 본인의 길이로 초기화 할 수 있다는 사실을 기반으로 dp[i] = 1로 초기화(기저 조건)할 수 있다는 것을 알 수 있다.

->또한, 방문한 원소의 위치의 모든 앞 원소에 대하여 부분 수열의 길이가 증가할 가능성이 존재(Arr[i] > Arr[1]...Arr[i - 1인 모든 경우)한다면, 해당 위치의 dp 테이블의 값에 + 1(본인의 길이)을 한 값이 dp[i]의 후보가 될 수 있다는 사실을 기반으로 점화식을 세울 수 있다. 즉 아래와 같은 식을 세울 수 있다.

 

3. 점화식을 바탕으로 dp 테이블을 갱신하면서 최종적으로 전체 문제를 해결한다.

->여기에서는 Knapsack Problem과 다르게, dp[N]의 값을 최종 답안으로 도출하면 안된다! dp 테이블의 정의를 다시 살펴보면 dp 테이블에 저장된 값은 해당 위치에서 '해당 원소가' 가질 수 있는 LIS의 값이었지, 해당 수열에서 가질 수 있는 LIS가 아니었다는 것에 주의해야 한다. 위의 예시에서 5, 6번째 위치를 바꿔 생각해보면 이해하기 쉽다. 아래 그림을 참고하자.

 

4. 구현

->지금까지 살펴본 바와 같이, 규칙성과 기억된 값(dp 테이블)을 적절히 활용하는 방법을 충분히 이해하였다면 코드를 작성하는 것은 매우 간단하고 쉬운 일이다. 아래 코드를 참고하도록 하자.

import java.util.Scanner;

public class LIS_DP1 {
	static int N;
	static int[] arr;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		arr = new int[N];
		for (int i = 0; i < N; i++) {
			arr[i] = sc.nextInt();
		}

		// 각 위치에서의 LIS를 저장할 1차원 dp 테이블을 정의한다.
		int[] dp = new int[N];
		// 최대 LIS의 값.
		int max = 1;

		// 첫 번째 원소부터 N번째 원소까지 dp 테이블의 값을 채워 나간다.
		for (int i = 0; i < N; i++) {
			// 우선 해당 위치를 본인의 길이(1)로 초기화한다.
			dp[i] = 1;
			// 현재 원소의 위치에 대하여, 앞의 원소의 값을 비교하며 값을 갱신한다.
			for (int j = 0; j < i; j++) {
				// 만일 부분 수열이 증가할 가능성이 있다면
				if (arr[j] < arr[i]) {
					// dp 테이블에 저장된 LIS를 바탕으로 가장 큰 값을 dp[i]의 값으로 갱신한다.
					dp[i] = Math.max(dp[i], dp[j] + 1);
				}
			}

			// 전체 수열에서 LIS의 값을 갱신한다.
			max = Math.max(max, dp[i]);
		}

		System.out.println(max);
		sc.close();
	}
}

->해당 로직을 이해했다면 알 수 있겠지만, 각 위치에서 모든 앞 원소를 참고하는 2중 for문으로 구성되기 때문에 O(N^2)의 시간 복잡도를 갖는 것이다.

 

*동적 계획법을 활용한 풀이 : O(NlogN)

->이번에 살펴볼 방법은 직관적으로 이해하기도 힘들고, 이분 탐색을 활용하기 때문에 난이도가 있는 풀이라고 할 수 있겠다. 그래서 이해가 잘 안 되는 것이 당연하지만.. 우선 아이디어의 컨셉부터 살펴 보자.

->앞선 방법을 이용하면, 각 원소의 위치를 조사할 때 마다 앞의 모든 원소를 탐색하는 과정을 거쳐야 했다. 따라서 O(N^2)이라는 시간 복잡도를 가지게 되었고, 이번에 사용하려는 방법에서는 앞의 모든 원소를 탐색하는 과정을 O(logN)까지 줄여볼 수 있지 않을까? 라는 물음에서 출발한다.

 

1. 문제를 특정한 부분 문제로 생각해보고, 해당 문제를 저장할 dp 테이블을 정의해본다.

(1) 현재 위치에서 부분 수열의 길이가 추가될 가능성이 있는가?

->앞의 해결 방법에서는 앞의 모든 원소의 크기와 비교하면서 현재 위치에서 부분 수열의 길이가 추가될 가능성이 있는지 파악하였다. 하지만 이 방법에서는 조금 다른 방법으로 그 가능성을 찾는다.

 

(2) 현재까지 조사한 앞 원소들에 대하여, 부분 수열을 만들 수 있는 최적의 수 조합을 저장해보자.

->예를 들어 i번째 원소를 조사한다고 생각했을때 1 ~ i - 1번째 원소에 대하여 i번째 원소가 부분 수열의 길이를 증가시킬 가능성이 있는지 생각하기 위해서, 1 ~ i - 1번째 원소에서 i번째 수가 부분 수열을 만들 수 있는 가능성을 쉽게 파악할 정보를 제공할 배열을 만든다는 이야기이다. 그런데 신기하게도 이 방법에서 이 배열은 만들어진다면 그 가능성을 쉽게 파악할 수 있을 뿐 만 아니라, 그 배열의 총 길이 자체가 LIS의 값이 된다!

->실제 테스트 케이스를 바탕으로 그림을 보면서 이해해보자. 우선 i번째 위치에서 1차원 dp 테이블에 채워진 원소의 총 길이는 '전체 수열에서 해당 위치에서 가질 수 있는' LIS의 길이를 의미하고, 원소의 값들은 i번째 원소가 부분 수열의 길이를 늘릴 가능성이 있는지 파악할 원소로 구성되어 있다. 여기에서 주의할 점은 앞 방법과 다르게 해당 위치에서 기록된 dp배열의 길이 그 자체가 전체 문제(최종 LIS의 값)의 최적해가 된다는 사실이다.

->우선 첫 번째 원소부터 생각해보면, 당연히 10이라는 값 자체를 dp[1]에 대입해주면된다. 그렇다면 테이블의 정의에 따라 1번째 원소에서 채워진 원소의 총 길이는 1로 LIS의 길이와 같고, 뒤에 조사할 수들이 부분 수열의 길이를 늘릴 가능성이 있는 정보를 제공해준다.

->다음으로 두 번째 원소를 생각해보자. 2번째 위치에서 LIS의 값은 2이기 때문에, dp[2]는 20을 채우는 것이 당연할 것이다. 또한 이 값들이 이후 3 ~ 6번째 원소의 부분 수열의 길이를 늘릴 가능성이 있는지 파악할 정보가 된다는 것을 기억하라.

->세 번째 원소부터가 중요하다. 우선, 우리가 아는 바로는 3번째 원소의 위치에서 LIS는 2가 되어야한다. 왜냐하면, 3번째 위치에서 전체적으로 가질 수 있는 LIS의 최대 값은 이전에 10, 20으로 구성된 부분 수열의 길이를 저장하면 되기 때문이다. 

 따라서, dp의 원소는 따로 조작할 필요가 없어보인다. 대신, dp에 구성된 원소는 다음 원소가 부분 수열의 길이를 늘릴 가능성이 있는 정보를 제공한다고 하였다. 우선 이해가 잘 안되겠지만, 현재 위치의 원소의 값이 dp에 저장된 값들 보다 같거나 작은 값이 있다면, 해당 값들 중 가장 작은 값의 위치와 원소를 교환하고 다음 과정을 진행한다고 알아두고 넘어가자.

->다음은 네 번째 원소이다. 우선, 4번째 위치에서 가질 수 있는 LIS는 3임을 알 수 있다(10, 20, 30으로 부분 수열이 구성됨). 따라서, dp[3]에 30이라는 값이 추가되는 것이 자연스러울 것인데 여기서부터는 어떤 규칙을 바탕으로 dp테이블에 원소를 넣는지 이해해보자.

 우선 우리는 지금까지 Arr 배열에 주목하여 30이 부분 수열의 길이를 늘릴 수 있는지 판단하였다. 하지만 앞서 말했듯이 뭔지는 모르겠지만 dp 테이블의 원소들의 값은 30이 부분 수열의 길이를 늘릴 수 있는지 판단할 정보를 제공하고 있다고 하였다. 우리가 Arr 배열을 보면서 판단한 정보는 부분 수열 10, 20이 현재 가장 긴 LIS를 갖는 수열임을 확인했을 것이다. 그런데 확인해보면 dp 배열에도 10, 20의 값이 저장되어 있음을 알 수 있다. 우리는 이 정보로부터 30이라는 숫자가 부분 수열의 길이를 늘릴 가능성이 있음을 파악할 수 있다. 그런데 여기서 주의할 점은, dp 배열에 저장된 값들이 현재까지 원소들을 조사하며 만들어진 LIS 배열 그 자체라고 생각하면 안된다.

->우선 5번째 원소에 대하여 dp배열을 계속 추가해보자. 마찬가지로, 해당 위치에서 가질 수 있는 LIS는 4일 것이고, 앞에서 구성된 부분 수열 중 가장 긴 부분 수열은 10, 20, 30으로 구성된 것으로 보아 dp[4]에 50이라는 값을 추가해주면 된다는 것을 알 수 있다. dp 배열에 저장된 원소를 확인해보면, 50이라는 값이 dp 배열에 저장된 모든 원소보다 큼을 알 수 있다.

->마지막으로 6번째 원소인 20을 다시 살펴보자. 이번에는 dp 배열을 참고해보았을 때, 저장된 값들 모두에 대하여 20이 크다는 보장이 없다. 3번째 원소때와 마찬가지로 현재 위치의 원소의 값이 dp에 저장된 값들 보다 같거나 작은 값이 있다면, 해당 값들 중 가장 작은 값의 위치와 원소를 교환하는 작업을 진행해준다.

->자, 어떻게든 이 과정을 따라오며 dp 테이블을 갱신하는 과정을 진행해보았고 결론적으로 dp에 구성된 원소의 길이는 4로, 우리가 구하고자 했던 LIS의 값 4와 일치한다는 것을 확인할 수 있다. 그런데 왜 이런일이 가능한 것일까?

 

(3) dp 테이블에 최적의 수 조합을 저장한다?

->앞 과정은 우선 dp 테이블을 갱신하는 과정이 어떻게 진행되는지 무지성으로 따라하며 보여준 것이고, 이번에는 테스트 케이스를 달리하여 이해해보도록하자. 아래 그림을 보자.

 앞서 갱신한 논리를 바탕으로 2번째 원소까지 dp 테이블을 갱신하면, 다음과 같은 값들을 저장함을 알 수 있을 것이다.

->그렇다면 바로 세 번째 원소 50에 대하여 갱신을 진행해보자. 앞선 논리를 바탕으로 한다면, dp에 저장된 모든 원소에 대하여 작은 부분 중 가장 작은 값의 위치와 해당 값을 바꿔줘야 하므로, 다음과 같이 갱신이될 것이다.

->네 번째 원소도 마찬가지로 갱신하면 다음과 같이 갱신이 될 것이다.

 만일 이러한 갱신이 진행되지 않는다면 어떻게 될까? 우선 직관적으로 보았을 때, 해당 수열에서 최종 LIS 배열은 {10, 15, 20, 30}으로 구성될 것을 알 수 있다. 그리고 우리는 dp 배열 만을 바탕으로 현재 위치의 수가 부분 수열의 길이를 늘릴 가능성이 있는지 파악하겠다고 하였다. 하지만 앞선 갱신과정이 진행되지 않는다면, 2번째 원소의 위치에는 100이라는 값이 저장되어 있을 것이고 뒤에오는 수인 15, 20, 30은 dp 배열만 보았을 때 부분 수열의 길이를 늘릴 여지가 없음을 알 수 있다.

 또 반대로 이런 갱신이 이루어 졌다면 2번째 원소의 위치는 위 그림과 같이 15로 갱신이 될 것이고, 그 뒤에 오는 수인 20, 30이 dp 배열만 보고도 부분 수열의 길이를 늘릴 여지가 있다는 것을 확인할 수 있다.

 따라서 이런 갱신을 진행해주는 것이다. 다만 이때 주의할 것은 저장된 원소가 LIS 배열 그 자체를 의미하지는 않는다고 하였다. 예를 들어 아래 수열을 바탕으로 LIS를 생각해보자.

 그림에서 확인해보면 LIS 배열은 {10, 20, 30}이 되는 것을 확인할 수 있는데, dp 배열에 저장된 수들과 일치하지 않음을 알 수 있다.

 

(4) 이게 왜 되는겨..?

->아무튼 이 과정들을 진행하면 최종적으로 dp 배열에 채워진 원소의 값들이 LIS 배열 자체를 의미하지는 않더라도, dp 배열의 길이 자체는 LIS의 길이가 됨을 경험적으로 확인할 수 있었다. 계속해서 강조하지만, 해당 배열의 길이는 LIS를 의미하지만 구성된 원소는 다음 원소가 부분 수열의 길이를 늘릴 수 있는 가능성을 보여줄 최적화된 정보라고 하였다. 이 사실을 잊지 말고 최근에 본 예시를 바탕으로 수열을 추가해보자.

 위에 제시한 예시에서, 마지막에 20이라는 수가 추가되었다면 같은 논리에 의하여 dp[3]의 값은 20으로 교체될 것이다. 여기서 우리는 교체 된다는 사실에 주목하여야 한다. 우선 어차피 '교체'가 일어난다면, 해당 dp 원소의 최종 길이(= LIS = 3)는 변화가 없을 것이다.

 두 번째는 정보 제공의 문제이다. 이 '교체'로 인하여 이후 추가될 원소들에게 부분 수열의 길이가 늘어날 가능성이 있는지 정보를 제공해주었다! 아래 그림을 참고하면 이해하기 쉬울 것이다.

 우리는 지금까지 {10, 20, 30}이라는 부분 수열을 생각하고 있었지만 해당 갱신으로 인하여 자연스럽게 {10, 15, 20}이라는 부분 수열이 이후 부분 수열의 길이를 늘릴 때 더 최적의 정보를 제공한다는 것을 알게 되었다. 

 즉, 가장 작은 증가 폭을 갖는 부분 수열을 시시각각 갱신해주는 것이 이후 부분 수열의 길이를 늘릴 때 유용할 것이고 어차피 교체가 일어나는 과정에서 LIS의 길이는 변화하지 않기 때문에 dp에 구성된 원소를 기준에 맞게 갱신하는 것은 상관없다는 것이다. 어떻게 이런 아이디어를 생각해 낸 것일까..? 난 못할듯..

 

2. 부분 문제의 관계를 생각하며 점화식을 도출한다.

->자, 앞의 규칙성을 이해하였다면 점화식을 도출하는 것은 역시 간단하다. 우선, 원소를 추가할 때 마다 현재까지 저장된 dp를 탐색하며 해당 원소보다 큰 값을 갖는 원소가 있는지 탐색한다. 

->이때 그런 값을 찾았다면, 그런 값들 중 가장 작은 값과 해당 원소의 위치를 교체해주고, 그런 값을 찾지 못했다면, dp 배열에 채워진 원소의 가장 마지막 부분에 해당 원소를 추가해주는 작업을 반복적으로 진행해주면 된다.

->이때, dp 에 저장된 원소들은 '오름차순'으로 정렬되어 있다는 사실을 알 수 있고 이 때문에 초기에 고려했던 앞 부분을 탐색하는 과정을 '이분 탐색'을 바탕으로 O(LogN)으로 줄일 수 있다. 따라서, 해당 알고리즘을 사용하면 시간 복잡도는 모든 원소(N개)에 대하여 탐색하는 과정을 O(LogN)만큼 반복하므로 총 O(NLogN)을 가진다는 것을 확인할 수 있다.

 

3. 점화식을 바탕으로 dp 테이블을 갱신하면서 최종적으로 전체 문제를 해결한다.

->초기에 설정한 바와 같이 최종 dp 테이블에 채워진 원소의 길이 = LIS임을 확인할 수 있다. 따라서 dp테이블에 실질적으로 저장된 원소의 값들의 길이를 출력해주면 된다.

 

4. 구현

->이 논리는 이해하기도 힘들고, 또 구현하는 과정에서 이분 탐색을 활용해야하기 때문에 구현하는 과정도 기존 dp에 비하여 간단하지 않다. 아래 코드를 참고하도록 하자.

import java.util.Scanner;

public class LIS_DP2 {
	static int N;
	static int[] arr, dp;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		arr = new int[N];
		for (int i = 0; i < N; i++) {
			arr[i] = sc.nextInt();
		}

		// dp에 실질적으로 저장된 원소의 길이 = LIS인 1차원 dp테이블을 만든다.
		// 해당 dp에 저장된 원소(0이 아닌 값)들은 이후 조사하는 원소들이 부분 수열을 늘릴 수 있을지에 대한 정보를 제공한다.
		dp = new int[N];
		// 처음에 저장된 원소는 없으므로, LIS = 0이다.
		int LIS = 0;

		// 첫 번째 원소부터 N번째 원소까지 dp 테이블의 값을 채워 나간다.
		for (int i = 0; i < N; i++) {
			// 이분 탐색을 활용하여 dp테이블에 저장된 원소를 탐색하며 현재 선택된 숫자가 dp테이블의 어떤 위치에 포함될지 파악한다.
			int idx = BinarySearch(arr[i], 0, LIS, LIS + 1);
			
			// 찾지 못한 경우
			if(idx == -1) {
				// 가장 마지막 위치에 원소를 삽입하고 LIS의 길이를 늘린다.
				dp[LIS++] = arr[i];
			}
			// 찾은 경우
			else {
				// 해당 위치에 현재 값을 삽입하여 갱신한다.
				dp[idx] = arr[i];
			}
		}
		
		// LIS의 길이를 출력한다.
		System.out.println(LIS);

		sc.close();
	}

	private static int BinarySearch(int num, int start, int end, int size) {
		int res = 0;
		while (start <= end) {
			// 중앙 값을 찾는다.
			int mid = (start + end) / 2;

			// 만일 현재 선택된 원소가 해당 원소보다 작거나 같다면, 앞 부분을 탐색한다.
			if (num <= dp[mid]) {
				// 해당 원소의 위치를 기억해둔다.
				res = mid;
				end = mid - 1;
			}
			// 만일 현재 선택된 원소가 해당 원소보다 크다면, 뒷 부분을 탐색한다.
			else {
				start = mid + 1;
			}
		}

		// dp테이블에서 삽입될 위치를 찾지 못한 경우(즉, 모든 수들보다 큰 경우).
		if (start == size) {
			return -1;
		}
		// dp테이블에서 삽입될 위치를 찾은 경우.
		else {
			return res;
		}
	}
}

->해당 문제의 최대 수열의 크기가 N이기 때문에 시간에서 큰 차이가 나지 않아보이지만, 입력 값이 클 수록 그 차이는 더 확연해 질 것이다.

1번 풀이 : 아래, 2번 풀이 : 위

 

※ 여기까지가 다이나믹 프로그래밍의 대표적인 예제인 LIS에 관한 설명이다. 오히려 Knapsack Problem보다 2번째 풀이에서는 격이 다른 어려움을 느꼈을지도 모른다. 계속해서 얘기하지만 당연하다. 사실 나도 잘 이해를 못하겠다 어떻게 이런 생각을 하는지.. 아무튼 이 문제로 부터는 정보를 어떻게 저장할 것이고, 그 정보를 어떻게 활용할 수 있느냐에 대한 인싸이트를 얻어볼 수 있다.