[Java]크루스칼 알고리즘(Kruskal Algorithm)

*크루스칼 알고리즘(Kruskal Algorithm)

-> 크루스칼 알고리즘은 그래프에서 최소 비용 신장 부분 트리(최소 신장 트리 : Minimum Spanning Tree(MST))를 찾는 알고리즘이다. 

※ 최소 신장 트리, 신장 트리와 같은 용어를 조금 더 자세히 알고 싶다면 위키백과를 참고하도록 하자.

ko.wikipedia.org/wiki/%EC%8B%A0%EC%9E%A5_%EB%B6%80%EB%B6%84_%EA%B7%B8%EB%9E%98%ED%94%84

신장 부분 그래프 - 위키백과, 우리 모두의 백과사전

 

*크루스칼 알고리즘의 매커니즘

-> 크루스칼 알고리즘은 기본적으로 그리디한 선택을 바탕으로 알고리즘을 진행한다.

(1) 주어진 그래프의 모든 간선에 대해서, 간선의 연결비용을 낮은 순으로 오름 차순 정렬한다.

(2) 정렬된 간선 순서대로 선택하면서, 간선의 양 끝 정점을 Union 한다. 단, 이때 선택된 두 정점이 같은 집합에 속해있다면 사이클(cycle)이 있다고 판단하고 포함시키지 않는다.

 이러한 매커니즘을 바탕으로 최종 선택된 간선을 연결한 것이 최소 비용 신장트리이다.

※ 크루스칼 알고리즘은 사실상 서로소 집합만 정확히 알고 있으면 매커니즘은 어렵지 않다. 서로소 집합에 대해서 먼저 명확히 이해하고 있어야만 한다. 서로소 집합에 대하여 잘 모른다면 아래 글을 참고하도록 하자.

sskl660.tistory.com/71?category=845232

[Java] 서로소 집합(Disjoint Set)(Union-Find)(Merge-Find Set)

-> 예를 들어 다음과 같은 그래프에서 최소 신장 트리를 찾아보도록 하자. 우선 첫 번째로, 연결된 간선의 연결 비용이 낮은 순으로 위에서 부터 오름차순 정렬하고, 다음 간선을 선택할때 사이클을 판단하기 위해 서로소 집합을 활용하기로 하였으므로, 각 노드의 초기 집합은 아래와 같을 것이다.

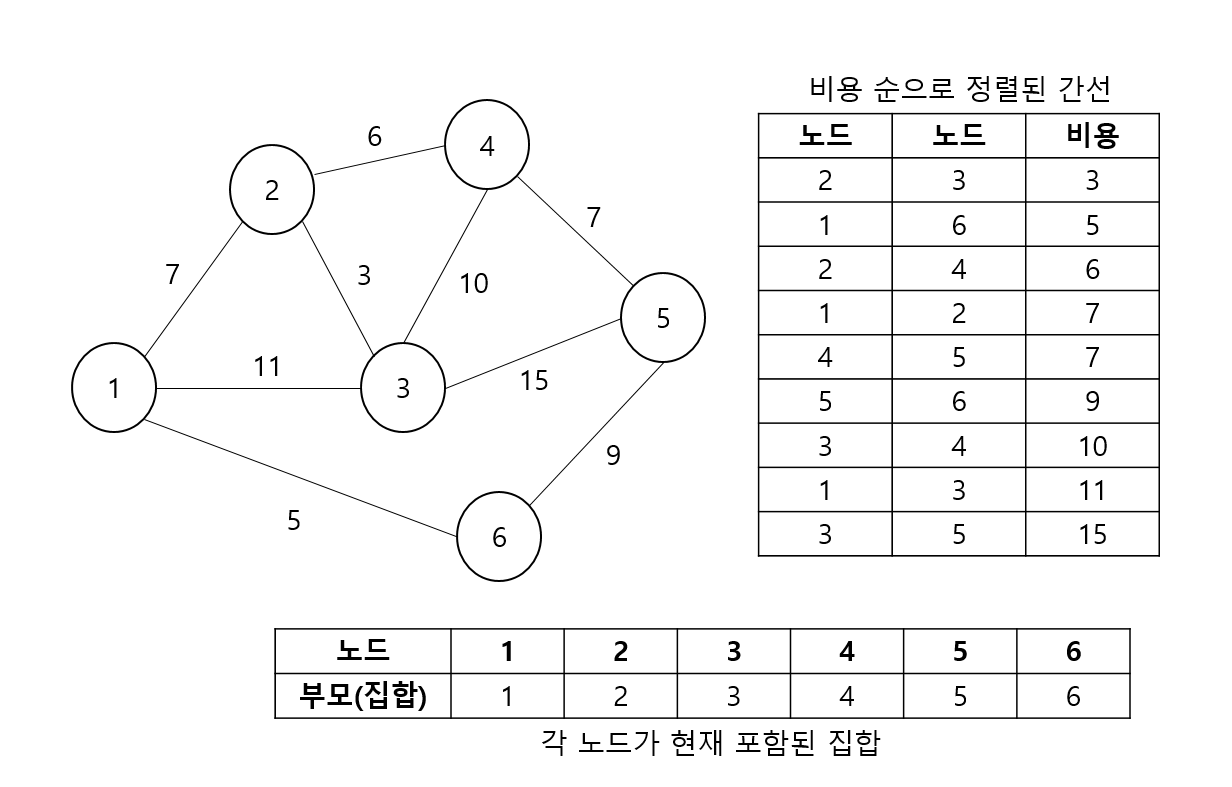
초기 상태

 그 다음은 말 그대로 비용이 적은 간선의 양 끝 노드를 선택하면서 사이클이 존재하지 않는다면 Union 및 해당 간선 선택, 존재한다면 스킵하는 형태로 모든 간선에 대하여 탐색이 끝날 때 까지 동작을 반복하면 된다. 아래 그림들은 이 과정을 나타내는 예시이다.

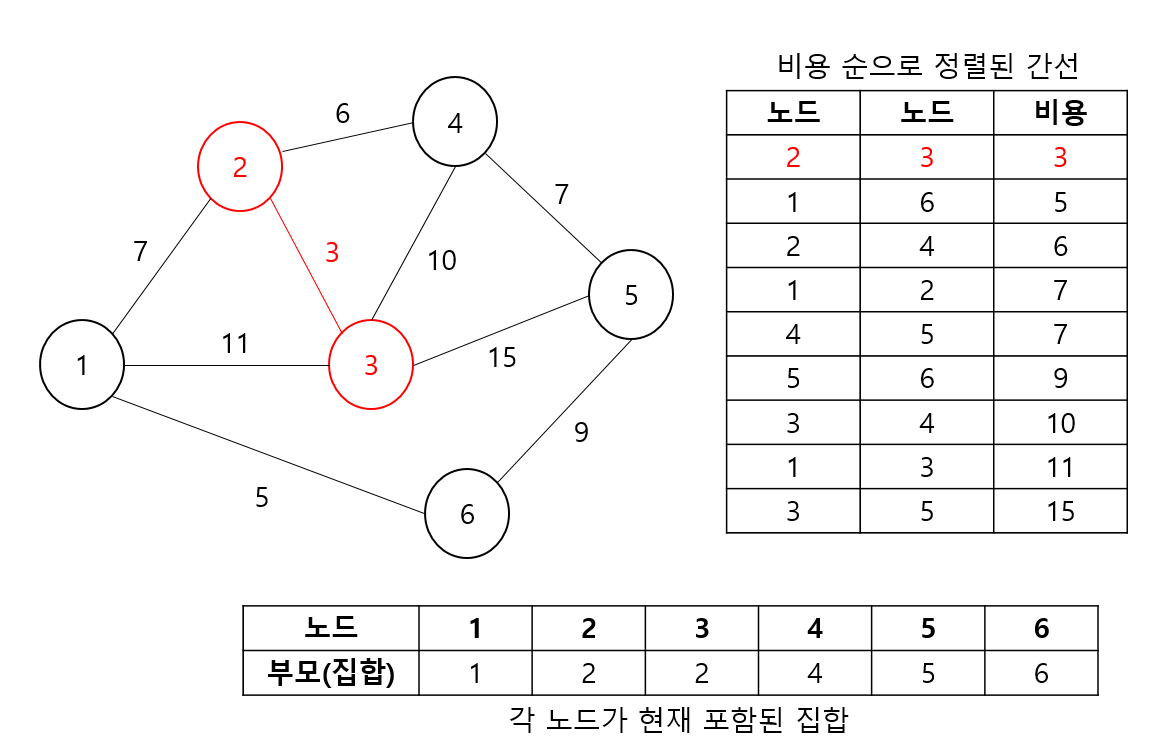
먼저, 첫 번째 간선을 선택한다. 두 노드 2, 3은 서로 독립된 집합이기 때문에 Union을 진행하고 간선도 선택한다.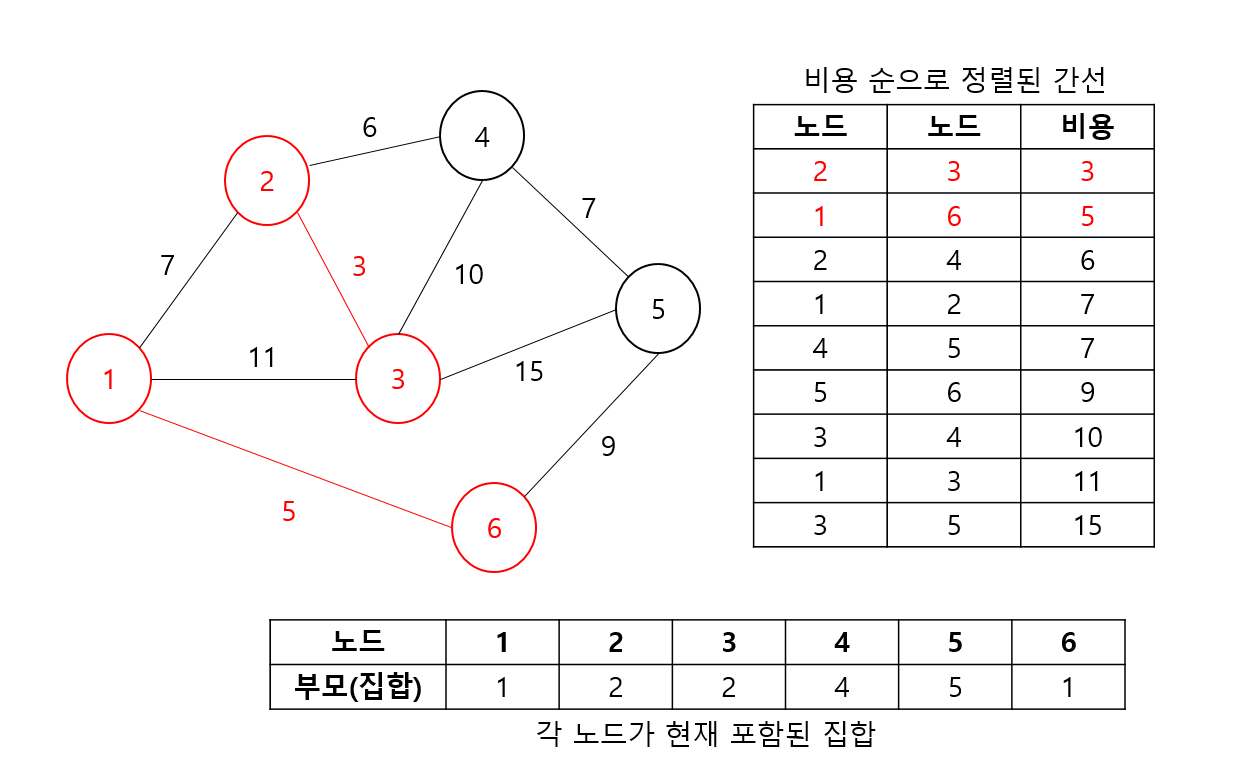

마찬가지 방법으로 두 번째 간선을 선택한다. 두 노드 1, 6은 서로 독립된 집합이므로 Union 및 간선을 선택한다.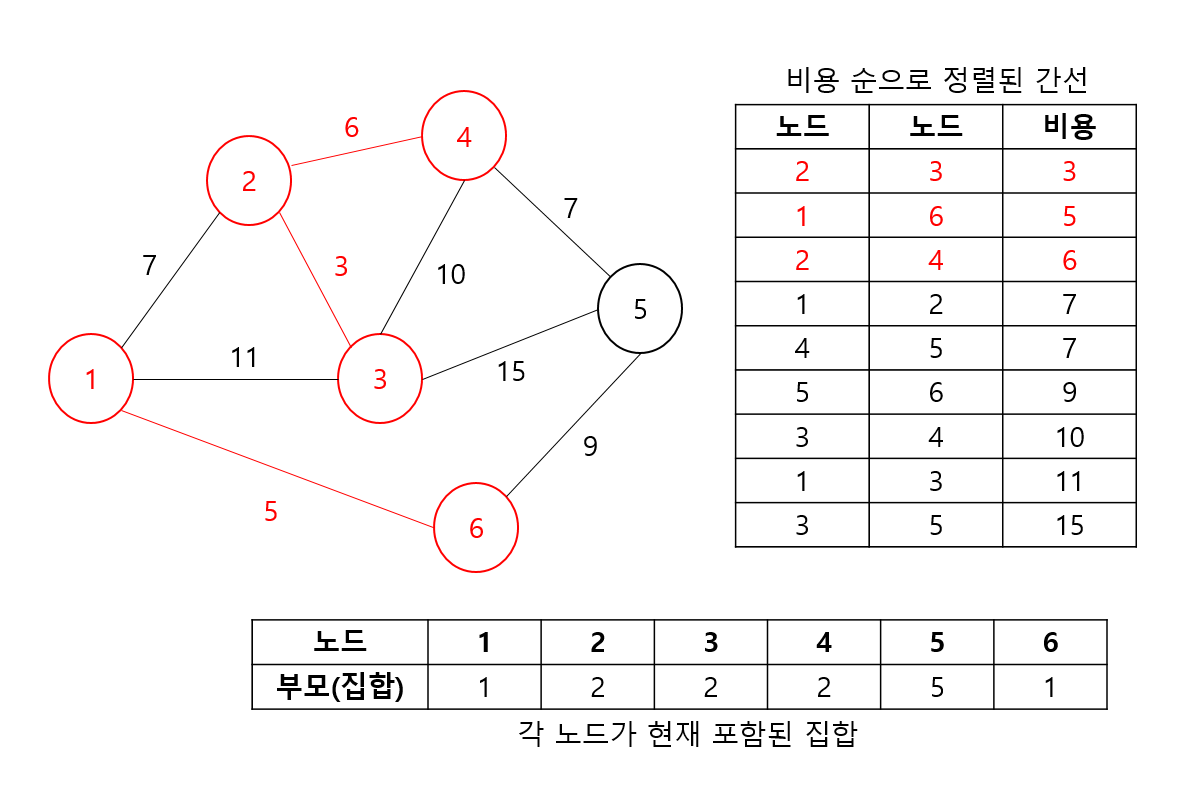 

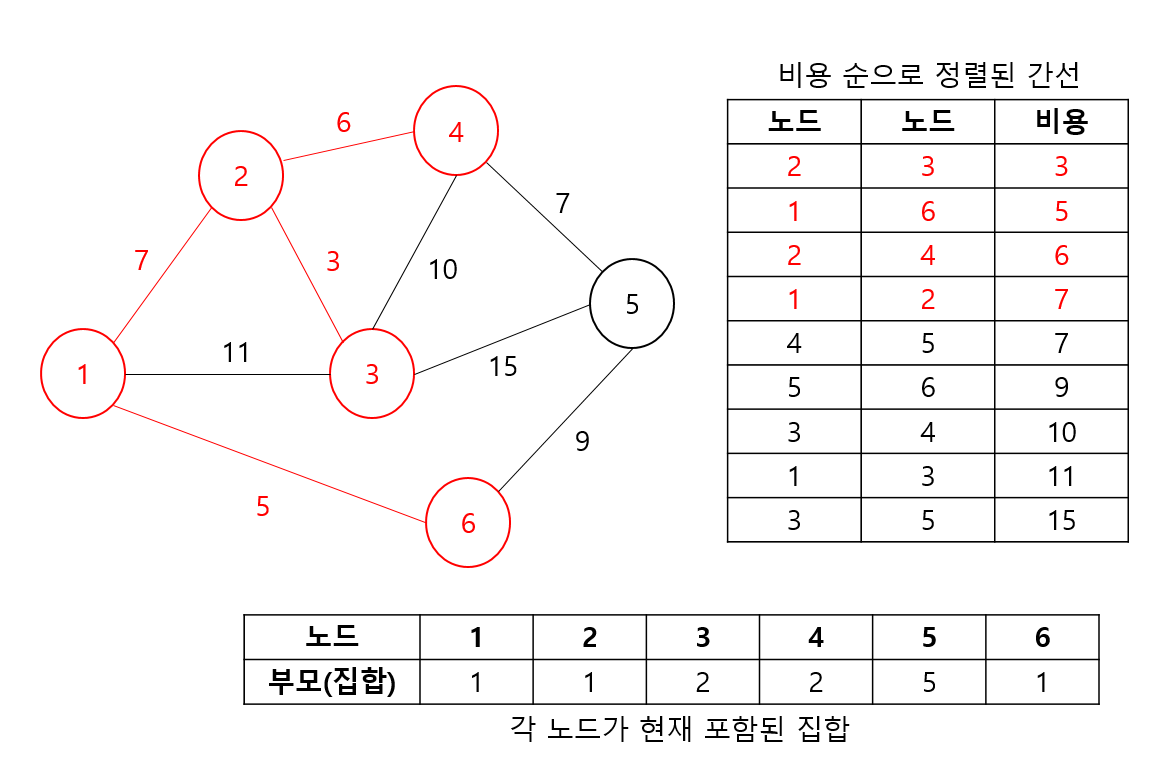
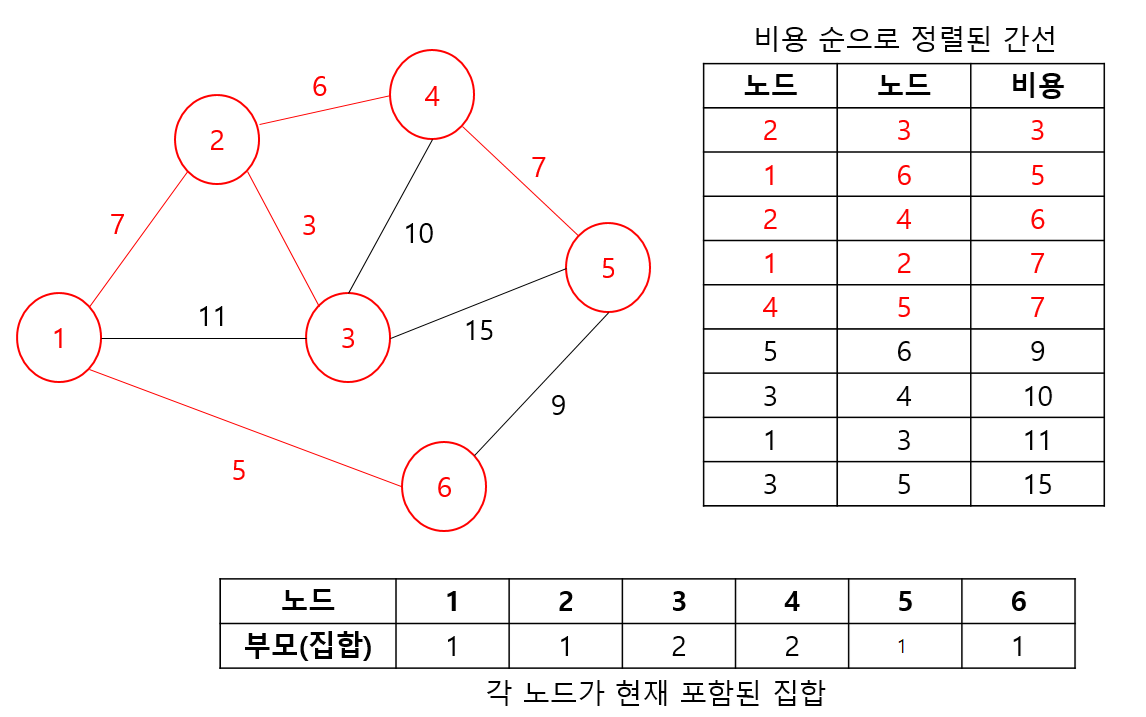
여기까지는 앞 과정과 다른 것이 없다.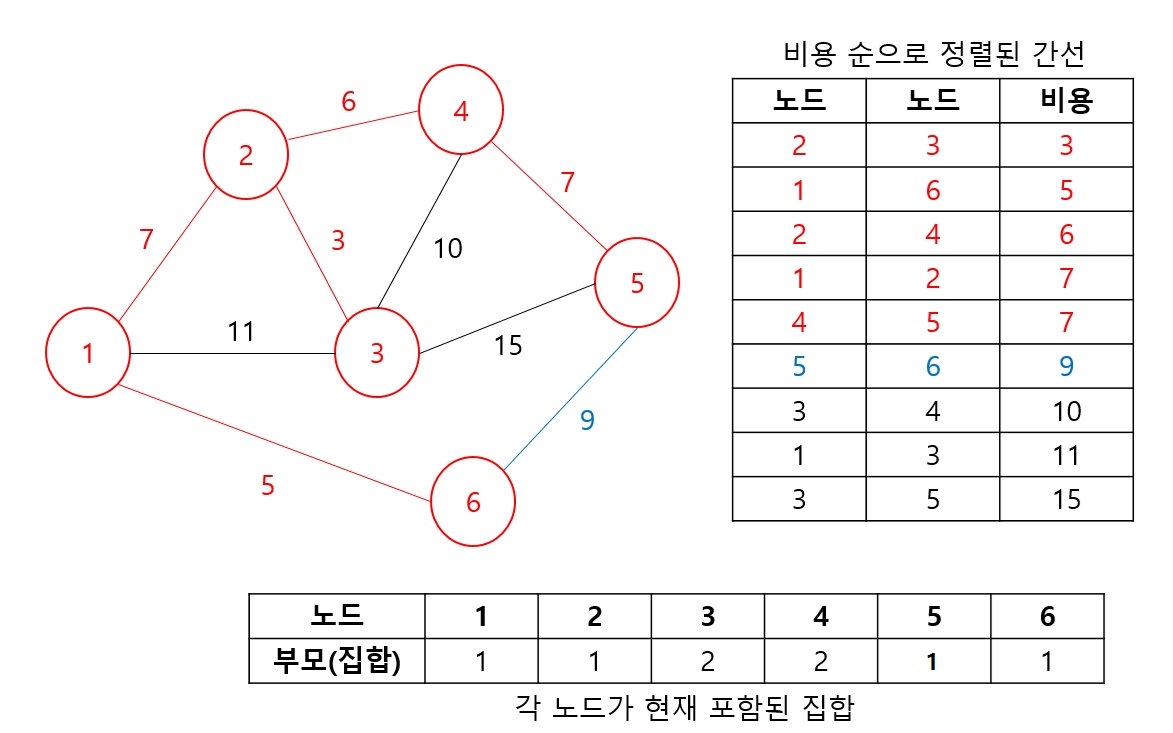

5, 6번 노드를 간선에 대해서는 각 노드 5번의 최종 부모는 1, 6번의 최종 부모는 1로 두 집합이 이미 같은 집합에 속해있음을 알 수 있다. 그림에서 확인해보면 알겠지만, 두 노드를 연결하는 순간 사이클이 발생한다. 따라서, 이 경우는 그냥 스킵하면 된다.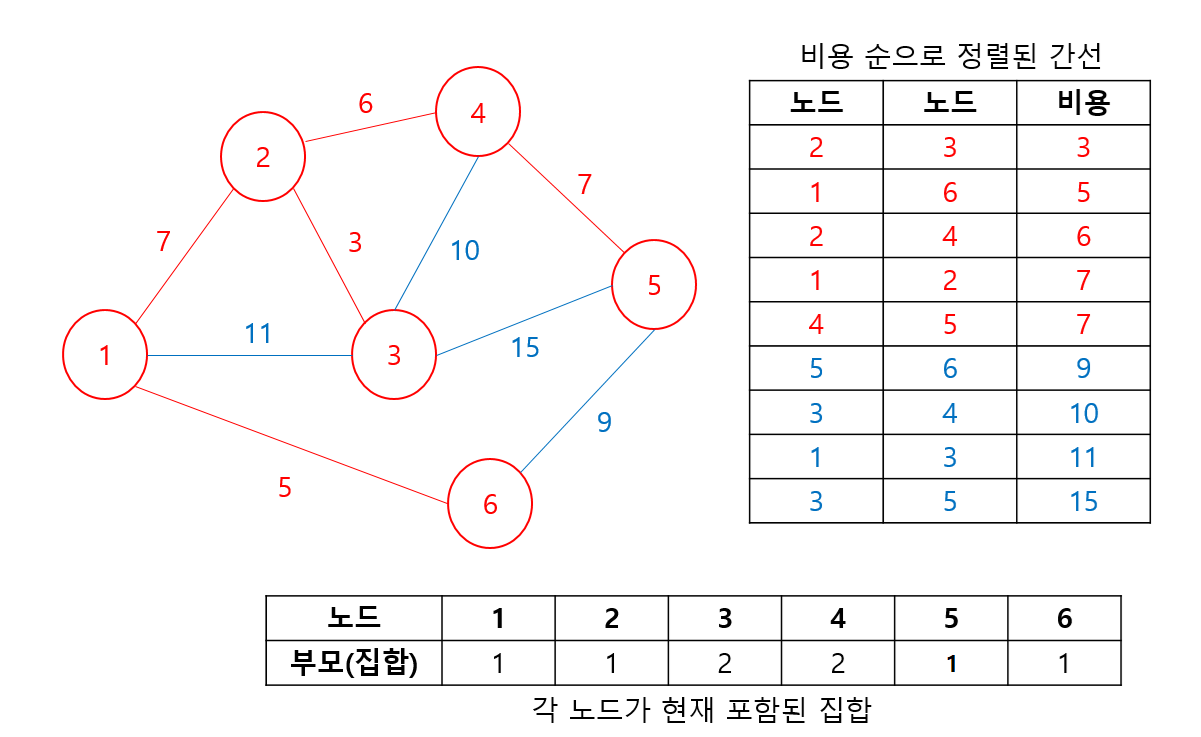

나머지 노드에 대해서도 마찬가지로 진행해주면, 최종적으로 선택된 간선(빨간색)이 최소 신장트리(MST)가 됨을 확인할 수 있다.

 

*크루스칼 알고리즘의 구현

-> 앞서 언급한대로 서로소 집합만 명확히 구현이 가능하다면, 크루스칼 알고리즘의 로직 자체는 크게 어렵지 않다는 것을 확인할 수 있다.

-> 위의 예시 그대로 크루스칼 알고리즘을 구현하면 아래와 같다. 보통 알고리즘 문제에서는 정렬된 상태로 주어지지 않기 때문에, 정렬되지 않은 상태로 입력을 주고 정렬하는 로직도 추가해 주었다.

import java.util.Arrays;
import java.util.Scanner;

/*
sample input(첫 줄의 첫 숫자는 정점의 개수, 두 번째 숫자는 간선의 개수).
6 9
1 6 5
2 4 6
1 2 7
3 5 15
5 6 9
3 4 10
1 3 11
2 3 3
4 5 7
 */

public class Kruskal {
	static int V, E;
	static int[][] graph;
	// 각 노드의 부모
	static int[] parent;
	// 최종적으로 연결된 최소 신장 트리 연결 비용.
	static int final_cost;

	public static void main(String[] args) {
		// 그래프의 연결상태(노드1, 노드2, 비용)를 초기화.
		Scanner sc = new Scanner(System.in);
		V = sc.nextInt();
		E = sc.nextInt();
		graph = new int[E][3];
		for (int i = 0; i < E; i++) {
			graph[i][0] = sc.nextInt();
			graph[i][1] = sc.nextInt();
			graph[i][2] = sc.nextInt();
		}
		parent = new int[V];
		final_cost = 0;

		// 간선 비용 순으로 오름차순 정렬
		Arrays.sort(graph, (o1, o2) -> Integer.compare(o1[2], o2[2]));

		// makeSet
		for (int i = 0; i < V; i++) {
			parent[i] = i;
		}
		// 낮은 비용부터 크루스칼 알고리즘 진행
		for (int i = 0; i < E; i++) {
			// 사이클이 존재하지 않는 경우에만 간선을 선택한다(여기서는 최종 비용만 고려하도록 하겠다).
			if (find(graph[i][0] - 1) != find(graph[i][1] - 1)) {
				System.out.println("<선택된 간선>");
				System.out.println(Arrays.toString(graph[i]));
				union(graph[i][0] - 1, graph[i][1] - 1);
				final_cost += graph[i][2];
				System.out.println("<각 노드가 가리키고 있는 부모>");
				System.out.println(Arrays.toString(parent) + "\n");
				continue;
			}
		}
		
		System.out.println("최종 비용 : " + final_cost);
		sc.close();
	}

	private static void union(int a, int b) {
		a = find(a);
		b = find(b);
		if (a > b) {
			parent[a] = b;
		} else {
			parent[b] = a;
		}
	}

	private static int find(int x) {
		if (parent[x] == x)
			return x;
		else
			return find(parent[x]);
	}
}

결과

※ Find 연산에서 경로 압축 기법을 사용하는 경우, 부모가 다르게 나올 수 있다. 경로 압축 기법을 명확히 이해 했다면 무슨 소리 인지 이해할 수 있을 것이다.

 

*시간 복잡도

-> 크루스칼 알고리즘은 O(ElogV)의 시간복잡도를 갖는다. 간단히 말하면 모든 가중치를 정렬하는데 걸리는 시간이 O(ElogE) 시간복잡도를 갖는데, 크루스칼 알고리즘에서 이 연산보다 영향력이 있는 연산은 없기 때문에 최종적으로 O(ElogE)가 걸린다고 생각하는 것이다. 이때, 간선의 수는 최대 V^2개가 될 수 있으므로 O(logE) = O(logV^2) = O(2logV) = O(logV)로도 볼 수 있고, 최종적으로 O(ElogV)의 시간 복잡도를 갖는 것이다.

-> 크루스칼 알고리즘의 자세한 증명과 시간 복잡도 증명은 위키백과를 참고하도록 하자.

ko.wikipedia.org/wiki/%ED%81%AC%EB%9F%AC%EC%8A%A4%EC%BB%AC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

크러스컬 알고리즘 - 위키백과, 우리 모두의 백과사전